A couple of days ago, writing in The Guardian, Tim Harford questioned and I quote
“Is our reliance on automation dangerously diminishing our skills?”
These days, we depend on Technology a lot and given our beliefs that a computer cannot go wrong, we accept the results without questioning the Math’s or the logic behind the answer.
Regardless of whether we are strong in the field of mathematics or not, most of us are able to do some simple calculation without the need to think too deeply on the subject. For instance, if I say that give I shall give you 12% on your money, you can easily calculate that if you gave me 1200 (we would generally use 100 / 1000, but using 1200 since it avoids decimals later), you will get 1344 at the end of one year (assuming that 12% is for a year). For ease, let’s refer to this as Lump sum.
But what if I told you that I shall take your money in installments and enable you to earn a XIRR return of 22.75%, can you calculate (even after taking the assistance of a computer) what your real returns will be? For ease, let’s refer to this as SIP.
Here is the thing. In both cases, you gave me 1200 Rupees and received 1344 at the end. But when it comes to knowing how much you earned, the difference between 12% and 22.75% is huge if not staggering.
But how do you end up getting that 22.75% and nope, it’s incorrect though it would be wildly inaccurate to compare a XIRR return with a CAGR return (or compare a returns generated by SIP over returns generated by lump sum investing).
We are generally used to relative comparison whether we use numbers or otherwise. When I say A is tall, it’s always relative to B or C who maybe shorter than A. But if D is taller than A, does that mean A is not tall?
Microsoft on its website describes XIRR as such;
Returns the internal rate of return for a schedule of cash flows that is not necessarily periodic. To calculate the internal rate of return for a series of periodic cash flows, use the IRR function.
In other words, when you have a series of fund flow that may or may not be periodic (SIP is generally periodic), this is a tool to calculate the Internal rate of Return.
Let’s return to our example I described above. If I take 1200 in lump sum from you and give you 1344 after one year, for a period of one year, you had no access to 1200.
On the other hand, if I asked you to give me 100 Rupees every month and end of the year retuned 1344, you would have earned an XIRR return of 22.75%. On the other hand, if I give you back 1277, I would have given you a XIRR return of 12%. Notice the difference?
The reason for that difference lies in the fact that after month 1, while in lump sum you have no money left in your hand, in the case of SIP, you still have 1100 that is yet to be given to me. At end of second month, you still owe me 1000 that you will give over the next 10 months. This money that you have has a value and the return using XIRR adjusts for that (theoretically speaking).
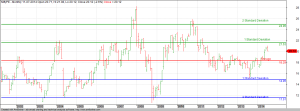
So, why am I talking about XIRR and CAGR returns? In recent times, Mutual fund houses and distributors have given a huge push to sell retail investors the idea of investing in Mutual Funds using Systematic Investment Plan. In itself, Systematic Investing is what we should do – whether its pushed or not. But when the push happens with the kind of returns as projected in the pic below, its setting up for disappointment

To showcase returns, most use XIRR as the tool to compare different schemes. So long, so good. But the problem is more on our side than the seller. Because of our unwillingness to use System 2 (Thinking, fast and slow by Daniel Kahneman), it’s easy to confuse XIRR with actual returns that we get. But think deeply and you shall see that what you see is not what you get.
When we invest in a Bank Recurring Deposit, our expectations are fixed. We invest X rupees for n months and at the end of the period we get Z. When we take a loan for a House or a Car, we know that we need to make a payment of X Rupees for n years and then the asset is ours (full and clear).
But when it comes to investing, especially investing in markets, the expectations and reality we face could be vastly different. Assume for instance that you started off a SIP in the month of May 2003 (you couldn’t have picked the bottom better than that). You keep investing a fixed sum of money without fail – you are prepared to wait for the long term.

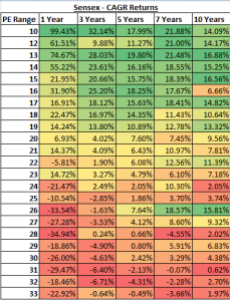
The correct way to depict returns would be as per pic which shows how much the investment of 72000 would have turned into (ignore last column which again is XIRR return). Picture courtesy (Pic-1 https://www.advisorkhoj.com, Pic-2 http://www.finvin.in/)
But then you get hit by the 2008 financial crisis. At the bottom with job loss being a worry, let’s assume you decided to take a look at what your investments have done. While markets have fallen, they are still 200% above where you started to invest. Your investments should have done well you assume and open up your account statement.
While you had invested for 70 months (let’s assume 10K per month) an amount of 700,000, your current value would be 816,887. Profit, yes but not something you would have expected. This again is due to the fallacy of comparing one sort of returns with another.
When we receive our final number, we quickly will use a calculator to see the return and would be horrified to see it gave a CAGR return of just around 2.65%. While the comparison is wrong (Apples to Oranges), the reason we fall upon it is because we understand the simplicity of it.
For the same values, if you use XIRR returns, you shall get the return as being 5.37% – low, but not as low as the CAGR we came up with.
While both are different, do note that either way, returns are way normal than what you may have expected. When mutual funds complain that a lot of investors stopped in 2008 / 09, the reason would be about their expectations not matching reality.
Mutual fund SIP returns are dependent on multiple factors (including market), but the three key things are
- How long you are investing
- When did you start (Starting date bias)
- When did you end
In the above example, returns would have been wildly different if you had started investing a few months later or stopped investing a few months later.
If you had started your investment say in Feb 2004 (one year later) and stopped in Feb 2009, your returns would be XIRR of 0.71% while in real terms, your 6,10,000 investment would have given you back 6,20,961.00
On the other hand, if you had stopped investing a year later (Feb 2010), your returns would be 19.71% while in real terms, your investment of 8,20,000 would be 16,01,760. A difference that is too big to ignore given the small change in time frames we tested with.
It’s easy for most of us to fall prey to availability bias (among our many other faults), but do remember that the final returns are not measured in either CAGR or XIRR but in what you finally receive in exchange for taking the risk.
Your expectations should be built on that reality alone since that is what we can finally compare and contrast easily. This is further and better explained by Utility of money. That is a big subject in itself, so shall leave you with this simple explanation taken from the site http://www.behind-the-enemy-lines.com/
If you want to read more about utility of money and its applications to portfolio management, insurance, and analysis of other cases, take a look at this book chapter.
PostScript: Both Pic-1 and Pic-2 contain similar info. Apologies for the confusion. Point I was trying to make is that you focus on the End Value vs comparing the % returns with other investment avenues you may have had the opportunity to invest in.